
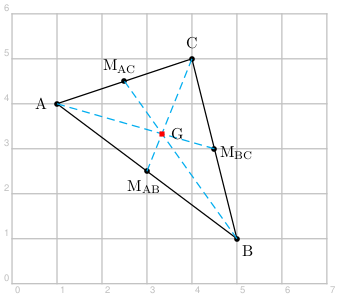
La commande \pstMiddleAB{A}{B}{M} crée le point M, milieu des points A et B.
La commande \pstCGravABC{A}{B}{C}{G} crée le point G, centre de gravité du triangle ABC.

|

|
| télécharger le code |
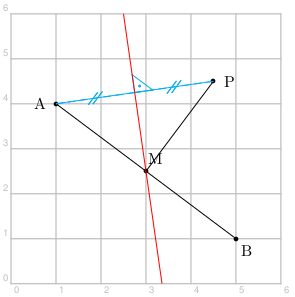
La commande \pstMediatorAB{A}{B}{M}{P} produit, à partir des points donnés A et B, deux autres points :
Les points M et P sont finalement reliés.

|
|
| télécharger le code |
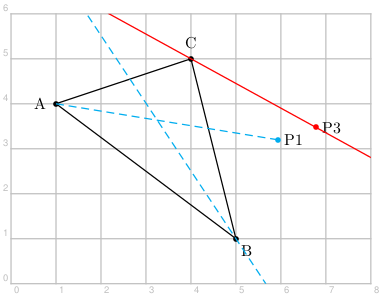
Les commandes \pstBissectBAC{B}{A}{C}{P} et \pstOutBissectBAC{B}{A}{C}{P} produisent le point P, situé sur la bissectrice, respectivement intérieure et extérieure, de l'angle BAC. Les points A et P sont ensuite reliés.

|
|
| télécharger le code |
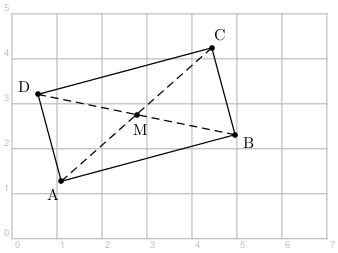
La commande \pstInterLL{A}{B}{C}{D}{I} détermine le point d'intersection I entre les droites AB et CD.

|
|
| télécharger le code |
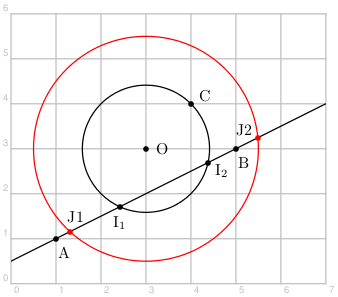
La commande \pstInterLC{A}{B}{O}{C}{I1}{I2} détermine les points d'intersection I1 et I2 entre la droite AB et le cercle centré en O et passant par C.
Tout comme pour la commande \pstCircleOA, l'argument pour le point C peut être laissé vide et le rayon ou le diamètre du cercle précisés avec les arguments optionnels Radius ou Diameter.

|
|
| télécharger le code |
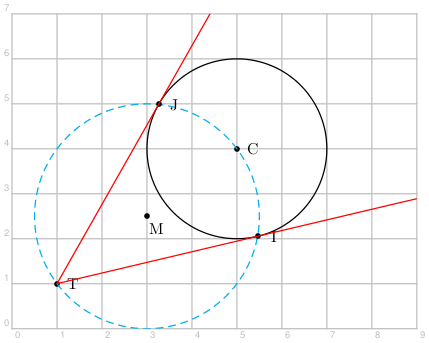
La commande \pstInterCC{O1}{C1}{O2}{C2}{I1}{I2} détermine les points d'intersection I1 et I2 entre le cercle centré en O1 et passant par C1, et le cercle centré en O2 et passant par C2.
Comme avec la commande précédente, les arguments pour les points C1 ou C2 peuvent être laissés vacants. On indique alors le rayon ou le diamètre de l'un ou l'autre cercle avec les arguments optionnels RadiusA, RadiusB, DiameterA ou DiameterB.

|
|
télécharger le code |
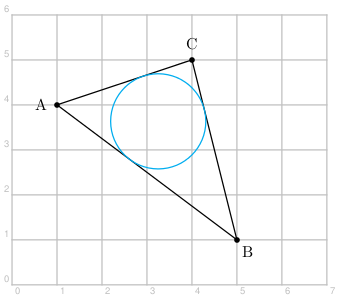
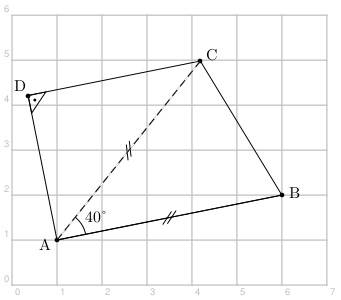
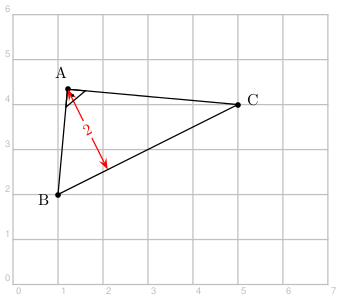
Construire les figures suivantes :
|
|
|